Der Raumwinkel wird mit der Maßeinheit Steradiant (Sterad, sr) angegeben.
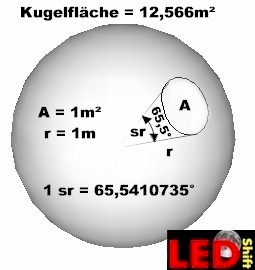Eine Kugel mit dem Radius von 1 Meter, besitzt eine Oberfläche von 12,566 m².
Wird jetzt auf der Kugeloberfläche eine Kugelkalotte (gewölbte Kreisfläche, Kugelsegment) von 1m² gezeichnet und man verbindet zwei Punkte, die 180° gegenüberliegend auf dem Umfang liegen, mit dem Kugelmittelpunkt, so umschließt dieser Kegel einen Winkel von 65,5°.
Dies sind dann 1 Steradiant oder auch Sterat sr genannt.
Genau genommen sind es 1sr = 65,5410735°...
Der Raumwinkel der gesamten Kugeloberfläche beträgt 4 x Pi = 12,566 sr und stellt somit bei 360° den größtmöglichen Raumwinkel dar.
Die Berechnung geht wie folgt: 4 x Pi x (sin x (X°/4))² = sr (siehe Tabelle)
Wer z.B. mit einigen SMD LEDs eine 360° Rundumbeleuchtung bauen will, sollte sich noch für den sr Anteil an einer Kugel interessieren.
Wenn eine SMD LED mit 65,5° ihr Licht abgibt (1sr), müsste man 12,566 dieser LEDs auf einer Kogeloberfläche gleichmäßig verlöten.
Die Anteile an der Kugeloberfläche werden von der Kugelkalotte so berechnet: Anteile = 2/1-cos(X°/2) (siehe Tabelle)
LED-Beleuchtung mit 1 Steradiant:
Ein LED-Leuchtmittel mit einem Abstrahlwinkel von 65,5° leuchtet 1 Sterat aus. Dieser Lichtkegel beleuchtet nach 1 Meter, die Fläche von 1m² in Form einer Kugelkalotte aus.
Wofür benötigt man den Steradiant in der LED-Beleuchtung?
Lux Angaben können in den Lichtstrom Lumen, und umgekehrt, umgerechnet werden.
Vorausgesetzt man kennt den Raumwinkel des Abstrahlwinkels des Leuchtmittels und den Abstand zur beleuchteten Fläche.
Um auf die beleuchtete Fläche zu kommen, muss der Abstand (r) zur Leuchtquelle zum Quadrat genommen werden und mit dem Raumwinkel des Abstrahlwinkels multipliziert werden.
A= r x r x sr Danach gilt: lm = A x Lux
Aber auch bei der Lumenberechnung aus der Beleuchtungsstärke, und umgekehrt, kann auf den Steradiant nicht verzichtet werden.
lm = cd x sr
| Öffnungswinkel: |
360° |
355° |
350° |
345° |
340° |
335° |
330° |
325° |
320° |
| sr Faktor |
12,5664 |
12,5634 |
12,5544 |
12,5395 |
12,4709 |
12,4174 |
12,3523 |
12,2756 |
12,1874 |
| |
| Öffnungswinkel: |
315° |
310° |
305° |
300° |
295° |
290° |
285° |
280° |
275° |
| sr Faktor |
12,0881 |
11,9777 |
11,8564 |
11,7246 |
11,5824 |
11,4301 |
11,2680 |
11,0962 |
10,9156 |
| |
| Öffnungswinkel: |
270° |
265° |
260° |
255° |
250° |
245° |
240° |
235° |
230° |
| sr Faktor |
10,7261 |
10,5280 |
10,3219 |
10,1081 |
9,8871 |
9,6591 |
9,4248 |
9,1844 |
8,9386 |
| |
| Öffnungswinkel: |
225° |
220° |
215° |
210° |
205° |
200° |
195° |
190° |
185° |
| sr Faktor |
8,6877 |
8,4322 |
8,1726 |
7,9094 |
7,6431 |
7,3742 |
7,1033 |
6,8308 |
6,5573 |
| |
| Öffnungswinkel: |
180° |
175° |
170° |
165° |
160° |
155° |
150° |
145° |
140° |
| sr Faktor |
6,2832 |
6,0091 |
5,7356 |
5,4631 |
5,1921 |
4,9233 |
4,6570 |
4,3938 |
4,1342 |
| |
| Öffnungswinkel: |
135° |
130° |
125° |
120° |
115° |
110° |
105° |
100° |
95° |
| sr Faktor |
3,8787 |
3,6278 |
3,3819 |
3,1416 |
2,9072 |
2,6793 |
2,4582 |
2,2444 |
2,0383 |
| |
| Öffnungswinkel: |
90° |
85° |
80° |
75° |
70° |
65,55° |
60° |
55° |
50° |
| sr Faktor |
1,8403 |
1,6507 |
1,4700 |
1,2984 |
1,1363 |
1,0003 |
0,8418 |
0,7099 |
0,5887 |
| |
| Öffnungswinkel: |
45° |
40° |
35° |
30° |
25° |
20° |
15° |
10° |
5° |
1° |
| sr Faktor |
0,4783 |
0,3789 |
0,2908 |
0,2141 |
0,1489 |
0,0955 |
0,0538 |
0,0239 |
0,0060 |
0,00024 |
| Öffnungswinkel |
360° |
270° |
240° |
220° |
200° |
180° |
160° |
140° |
120° |
100° |
| Teile einer Kugel |
1 |
1,172 |
1,333 |
1,490 |
1,704 |
2 |
2,420 |
3,040 |
4 |
5,599 |
| |
| Öffnungswinkel |
90° |
85° |
80° |
75° |
70° |
65,541° |
60° |
55° |
50° |
45° |
| Teile einer Kugel |
6,828 |
7,613 |
8,549 |
9,678 |
11,059 |
12,566 |
14,928 |
17,701 |
21,346 |
26,274 |
| |
| Öffnungswinkel |
40° |
35° |
30° |
25° |
20° |
15° |
10° |
5° |
1° |
|
| Teile einer Kugel |
33,163 |
43,212 |
58,695 |
84,374 |
131,646 |
233,778 |
525,582 |
2101,33 |
52525,23 |
|
|
www.LED 
.com
